time dynamics of insulation
So we’ve been having well-nigh to “design days” mixed with
unseasonably warm bursts in the Boston area lately, and a few
days ago I noticed an odd phenomenon. The heat pump is “correctly
sized” here, e.g. will run most of the time over those nights
below 5F, so its runtime percentage reflects the short-term heat
loss of the house fairly well. On a day when it was cold overnight
and then shot up to 35 or more during the next day, the pump
basically never ran for the entire afternoon which seemed odd
because there was still a substantial delta-T from inside to
outside and some quantity of loss must still be occurring.
Then it got cooler into the evening and things started getting
back to normal. The day was cloudy, so solar influence could
be mostly eliminated as a factor.
This got me thinking about the gradient through the 4 inches
of polyiso on the walls and what it might look like at any
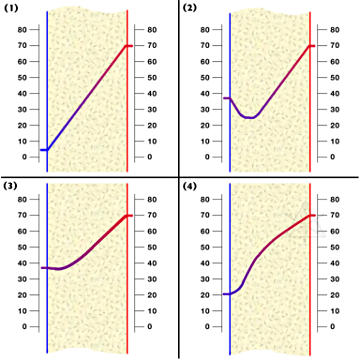
specific time during these events. I doodled up a representative
graphic, assuming a uniform wall of nothing but polyiso foam:
[Click the pic or label for a detailed version — it doesn’t
look like <img> tags work on this site anyways. Fix pls??]
In state (1) we have the steady-state wikkid-cold, in which a
fairly uniform gradient should be present through the wall.
Then the daytime temp goes up fairly rapidly with the interior
unchanged, which should begin heating the exterior of the wall
but it would take a while for that new temperature to penetrate
inward through the outer part of the polyiso and possibly look
something like frame (2). Now, the polyiso doesn’t have a lot
of heat *capacity* like brick or stone, so the quantities of heat
flow per time should track the gradient fairly closely. The
question then is, exactly what is going on in frame (2)? Since
the gradient from the freshly-warmed outside implies *inward*
heat flow, then there cannot be any net heat loss from the
building while this condition exists.
Now, how long would that condition last? With the outdoor temp
sustained at the warmer level the gradient would have to start
equalizing itself as in frame (3), and the secondary question is
how long would that take through a known thickness of polyiso
foam. In this case it seemed to take several hours, the time
over which the heat pump didn’t run at all. In frame (4) we’re
into evening as the temps drop and the gradient that was trying
to equalize to the warmer outdoor temp gets even more complex
as the changes might reflect as a very damped response depending
on how far along the gradient we look, almost like if we shook
one end of a flexible rope sitting in a viscous medium.
Does this make sense? I guess what I’m asking is what the
effective time constant of polyiso foam is, given that it must
have almost no heat capacity [e.g. specific heat * mass] of
its own. Are there whitepapers on this somewhere?
_H*
GBA Detail Library
A collection of one thousand construction details organized by climate and house part
 [Image]
[Image]






Replies
The thermal mass of polyiso is miniscule- the effects you are most likely seeing is the combination of solar gain (even through clouds) and the increased plug loads and human-heat emittance during waking hours. On a sunny day in Boston even moderate-R houses (R20-ish whole wall) are running a BTU surplus.
The thermal mass effect is (somewhat) measurable in higher-R cellulose walls, due to the much higher thermal mass of cellulose. The specific heat of paper is 0.33 Btu/lb-degree-F, and in a foot thick (R40-ish) dense packed wall you're looking at about 3.5lb per square foot of wall, or about 10 BTU per degree-foot. That's not exactly a mass-wall, but it's not nothing. The specific heat of polyiso is comparable, at about 0.30 Btu/lb-degree-F but foil-faced iso is 1.5lbs/cubic foot nominal, and at your R25-ish 4" you're looking at 1/3 of a cubic foot, or 0.5lbs per square foot. That's 1.5 BTU per square foot per degree.
Apples-to-apples, at the same ASTM C 518 rated R, you're looking at about 6 BTU/degree-foot for R25 cellulose, or 4x that of R25 polyiso.
You can model this as distributed capacitance distributed resistance lossy transmission line or a chain of R/C filters to get the prop-delay on temperature step functions, but the mass effect of the insulation layer of even the fat cellulose wall is small compared to what's going on with the solar gain and thermal mass of all the stuff inside the house.
Note, with polyiso the outer inch or two of foam is running about R2-R3/inch when the outdoor temps are below +5F, but rises to the R5/inch range when it's +35F outside, an artifact of it's very non-linear derating curve that falls off a cliff at middle-foam-depth temps below 25F, so it's underperforming by quite bit at the temperature extremes, but performing pretty well when it's above freezing out. That is going to be a much more dramatic effect than any mass-modeling of the iso. Peak-performance of iso occurs when the middle-foam-depth temp is ~50F. In a Boston climate with a 4" foam stackup you'll get somewhat better winter-average performance out of 1.5" of EPS on the exterior with 2.5" of polyiso between the EPS and structural sheathing, since EPS performance approaches R5/inch at 0F middle-of-EPS layer temps (R4.5/inch @ 40F middle-depth temps.)
https://www.greenbuildingadvisor.com/sites/default/files/Karagiozis%20-%20thermal%20conductivity%20of%20a%20variety%20of%20insulations%20as%20a%20function%20of%20mean%20temperature.jpg
https://www.greenbuildingadvisor.com/blogs/dept/musings/cold-climates-r-5-foam-beats-r-6
Heh, so my *steady-state* gradient at 5F or less outdoors probably
looks more like frame (4), huh?
Thanks for applying the perspective. I remember the "R5-beats-R6"
thread but I must have read it quite a while ago and I see now
that much of its comment thread is more recent. It possibly
helps explain a couple of other things on the house here too.
That and I'm starting to believe I'm seeing fairly profound
effects from night-sky radiation off the silver-painted metal
roof and to some extent from the vinyl siding, lowering the
effective outdoor temp at the polyiso face. Maybe it's time to
get some actual temp sensors embedded into parts of this rig...
and be even more glad we never did *any* cavity-fill in the
original walls. Perhaps if the outer 2" layer had been done
in XPS instead??
Anyway, I didn't think there would be much time dependency
here but I thought the cold-warm-cold day pattern might have
had the heat running a *little* more than it did over the
peak. And it was fun to doodle up the gradient graphic..
_H*