At first glance, the word “flux” looks like it may not be appropriate in polite company. In fact, though, it’s a word used in physics all the time. Flux comes from the same Latin root that gives us “flow.” The two are still intimately connected because things that flow can be quantified by their flux. And that’s where building science comes in.

You may have already dealt with flux and not realized it. One of the fundamental principles of building science is controlling the flow of moisture, air, and heat. Let’s zero in on heat. When we talk about heating or cooling loads, we specify them—using those annoying imperial units—in British Thermal Units per hour (BTU/hr). That’s a rate characterizing the flow of heat per unit time.

Taking it a step further, we can divide the time rate of heat flow by the area that it flows through. For heat, we’d end up with BTU per hour per square foot (BTU/hr/sf). And that quantity is the heat flux. But it doesn’t stop with heat. We can calculate the flux of air, moisture, electric field, energy…anything that flows. That’s all there is to it. (Well, OK, there may be a bit more to it, but this isn’t the place for a lesson on vector calculus.)

I was reminded of this recently when I was reading some old research papers from the Florida Solar Energy Center about attic ventilation as I was preparing my article on powered attic ventilators. One of the things they studied back in the 1980s and ’90s was the heat flux through the ceiling for attics under various conditions: unvented, passively vented, and power vented. Naturally, the reason behind the studies was that everyone—building scientists, occupants, and especially the people who have to go up there—wants to get the flux out of the attic.

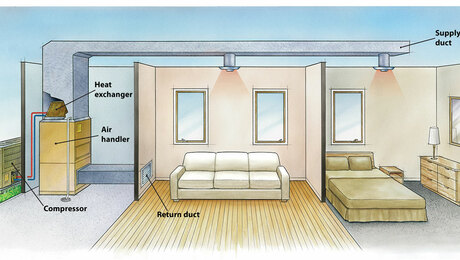
As mentioned above, we can calculate the flux for any quantity that flows. Air flow is another important building science concern. The result of a blower door test is an air flow rate: cubic feet per minute at 50 Pascals of pressure difference (cfm50). We can factor in the size of the building in various ways, but one of the best is dividing the air flow rate by the building enclosure surface area. The (I-P) units for this would be cfm50 per square foot, and that tells you the air flux through the building enclosure. Phius uses that as a passive house metric for airtightness.

Now, whether you wanted to or not, you know this term that occasionally pops up in building science. Feel free to use it in polite—or other—company and explain the intricacies of moisture, air, and heat flow through surfaces.

If we lived in 14th century Europe, you would probably want to be careful how you used the term. Apparently it meant “abnormally copious flow” back then, and given what we know about how weird those people were, you might end up watching the flux of your blood into the barber’s bucket if you said the wrong thing.

____________________________________________________________

Allison Bailes of Atlanta, Georgia, is a speaker, writer, building science consultant, and the founder of Energy Vanguard. He has a PhD in physics and writes the Energy Vanguard Blog. He is also writing a book on building science. You can follow him on Twitter at @EnergyVanguard.